Кейс. Управление запасами на оптовом складе

Оптовая торговая компания продает импортный алкоголь.
Вино «Don Simon» продается в среднем в количестве d = 100 коробок в день, судя по месячным продажам. Разумеется, день ото дня спрос варьирует.

Менеджер заказывает товар партиями по 3000 коробок у крупного поставщика один раз в месяц. Практика показывает, что поставщик выполняет заказ (доставляет заказ на склад) через L = 16 дней после поступления заявки. Менеджер стремится, с одной стороны, не уменьшать оборачиваемость товара и не делать излишних запасов, а с другой стороны, он не хотел бы устраивать дефицит товара, когда запасы вина заканчиваются до поступления новой партии.

Как в идеале должна выглядеть схема управления запасами для «Don Simon»?
Сколько в среднем товара X_L будет востребовано за время L ожидания новой партии?
Менеджер хочет держать риск возникновения такой ситуации, когда товара на складе не хватит до прихода новой партии на уровне α = 10% (5% 1%). Сколько товара менеджер должен иметь на складе в момент подачи заявки на новую партию товара?

1

Идеализированные модели управления запасами

В управлении запасами используют две базовые модели: Модель заданного размера заказа и Модель заданного периода между заказами

d — спрос в единицу времени (н-р, количество прооданных единиц за день)
L — срок исполнения заказа (срок поступления заказанного товара на склад)
T — время до следующего заказа (период между заказами)
I — остаток товара на складе
Q — размер заказа

fixed order quantity system, FOQS

Заказ заранее запланированной партии товара размером

Q = d * T

делают, как только на складе осталось

ROP = d * L

единиц товара. Re-Order Point - точка перезаказа

при постоянном среднедневном спросе d = 100 ед./день и сроке доставки товара от поставщика L = 16 дней при достижении на складе остатка ROP = 100*16 = 1600 единиц
менеджер делает заказ партии товара Q = 100 *30 = 3000 единиц.

если ежедневный спрос выше среднего дневного спроса, то остатки склада достигают величины ROP быстрее, и заказ делается раньше;
если ежедневный спрос вдруг становится меньше, то товарный запас на складе достигает величины ROP медленнее, и заказ делается позже.

fixed order interval system, FOIS

Заказ делают в заранее запланированное время, но размер заказа определяется по формуле

Q = d * T + d * L - I

т.е. расчитывается потребность в товаре на весь срок

T + L

до следующей возможной коррекции запаса и из нее вычитается уже имеющийся запас I.

раз в месяц T = 30 дней при постоянном среднедневном спросе d = 100 ед./день и сроке доставки товара от поставщика L = 16 дней и остатке на складе I = 1600 единиц (именно столько нужно, чтобы товара хватило до прибытия новой партии)
менеджер делает заказ партии товара Q = 100 *30 + 100*16 - 1600 = 3000 единиц.

Если ежедневный спрос увеличивается, то менеджер через время T сделает больший заказ Q.
Если ежедневный спрос становится меньше, то менеджер уменьшит заказываемую партию товара Q.

Как видим, в идеализированном варианте обе модели дают совершенно одинаковый результат. Вторая модель с фиксированным Т необходима при управлении группой товара, поставляемого от одного поставщика одной партией.

Однако в реальности спрос не фиксирован. Даже если в среднем за день продается 100 единиц товара, то день ото дня продажи различаются.

Из-за вариативности ежедневного спроса реальные диаграммы остатков склада будут не такими идеальными.
Рассмотрим, как могут меняться остатки склада после того, как менеджер сделал заказ.
Иногда товар на складе будет заканчиваться до прибытия новой партии. Такие участки показаны на диаграммах красным цветом. Иногда на складе будет оставаться товар, и после прибытия новой партии товара на складе будет не 3000 единиц, а больше.

Диаграммы остатков склада в разных схемах управления запасами

если реальный спрос был ниже среднего, то на складе останется нераспроданная часть товара, так образуются образуются остатки;
если реальный спрос был выше среднего, то на складе будет распродан весь товар, спрос остается неудовлетворенным и возникает дефицит. На диаграммах этот "отрицательный запас", выделенный красным цветом.

Итак, остатки склада и дефицит товара на складе определяются изменениями спроса.

Важные вопросы управления запасами:

Как часто к моменту доставки новой партии товара возникает его дефицит (склад пуст)?
Из определения среднего следует, что спрос в половине случаев выше среднего, а в половине случаев ниже среднего, поэтому риск дефицита возникает в 50% случаев.
Вероятность возникновения риска дефицита на складе равна 50%.
Каким образом можно уменьшить риск дефицита, сделать его ниже 50%?

Ответ на этот вопрос, в общем, очевиден. Нужно заказывать новую партию раньше.
Это означает, что будет создан так называемый резерв безопасности (safety stock).
Создание безопасного резерва означает увеличение среднего уровня запаса на складе, что повлечет за собой увеличение издержек хранения.
Это - плата за снижение риска возникновения дефицита.

Какова величина этой платы?
Как оценить риск возникновения дефицита и соответствующую величину безопасного резерва?

На последние два вопроса мы ответим позже. Сейчас понятно, что идеализированные схемы управления запасами нужно поправить на величину безопасного резерва SS.

2

Реальные модели управления запасами

Пусть SS - величина безопасного резерва.
Введем эту величину в идеализированную модель управления запасами.

fixed order quantity system, FOQS

Заказ заранее запланированной партии товара размером

Q = d * T

делают, как только на складе осталось

ROP = d * L + SS

единиц товара. Re-Order Point - точка перезаказа, SS - страховой резерв

Если спрос за время L будет ниже среднего, то на момент прибытия новой партии товара запас склада будет выше SS.
Если спрос за время L будет равен среднему, то на момент прибытия новой партии товара запас склада будет равен SS.
Если спрос за время L будет выше среднего, то на момент прибытия новой партии товара запас склада будет ниже SS.

fixed order interval system, FOIS

Заказ делают в заранее запланированное время, но размер заказа определяется по формуле

Q = d * T + d * L - I + SS

т.е. расчитывается потребность в товаре на весь срок до получения следующей через период партии товара

T + L

и из нее вычитается уже имеющийся запас I и добавляется страховой резерв SS.

чем больше безопасный резерв, тем меньше риск возникновения дефицита товара на сладе
чем меньше безопасный резерв, тем больше риск возникновения дефицита товара на сладе
если безопасного резерва нет, то с вероятностью 50% возникнет дефицит.

Таким обазом, схему управления запасами на нашем оптовом складе можно изобразить на следующей диаграмме.

Диаграмма остатков склада при схеме управления запасами, учитывающей безопасный резерв

Введение безопасного резерва существенно снижает риск возникновения дефицита. При этом вероятность возникновения дефицита становится меньше 50%.

Как подобрать величину безопасного резерва?

Чем больше безопасный резерв, тем меньше риск дефицита. Мы можем установить безопасный резерв таким, что риск дефицита будет нулевым.
Но чем больше безопасный резерв, тем больше денег замораживается в товарных остатках на складе, а значит тем ниже становится оборачиваемость денег, вложенных в запасы товара.
- экономически просчитать величину безопасного резерва;
- найти соотношение между величиной безопасного резерва и величиной риска дефицита.

Если мы хотим снизить риск дефицита до 5%, то какой безопасный резерв нужно назначить?
Очевидно, что величина безопасного резерва будет зависеть от спроса. Но спрос - величина случайная.

3

Как описать случайный спрос

Здесь нужно вспомнить теорию вероятности.

Опсание случайной величины. Среднее значение и стандартное отклонение.

Случайная величина - это величина, конкретное значение которой в данном конкретном случае нам неизвестно, но мы знаем, какие значения она может принимать, и знаем, каковы вероятности тех или иных значений.
Мы не можем точно предсказать результат одного испытания, связанного с этой случайной величиной, но можем довольно надежно предсказать совокупность результатов большого числа испытаний.
Чем больше испытаний, тем точнее наши предсказания.

какие значения может принимать случайная величина;
каковы вероятности этих значений.

Таким образом, мы можем задать случайную величину X в виде таблицы распределения случайной величины.

Возможные значения X	x₁	x₂	x₃	x_n
Вероятность	p₁	p₂	p₃	p_n

возможные значения x₁, x₂, x₃, x_n, вообще говоря, могут быть любыми;
вероятности p₁, p₂, p₃, p_n должны быть больше 0, а их сумма равна 1.

Мы можем описать случайную величину формулами:

	Среднее значение	Стандартное отклонение	Коэффициент вариации
Математическая формула
Функция Excel

Таким образом, для случайной величины можно вычислить среднее значение и стандартное отклонение. Напомню, что стандартное отклонение характеризует величину разброса точек выборки вокруг среднего значения.
Однако эти характеристики не являются исчерпывающими. Этот факт легко продемонстрировать на примере диаграмм, приведенных ниже.

Сложности в описании случайных величин

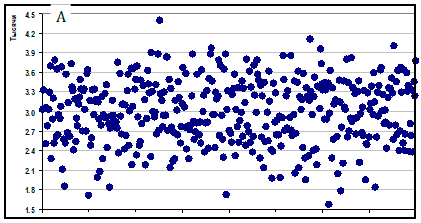
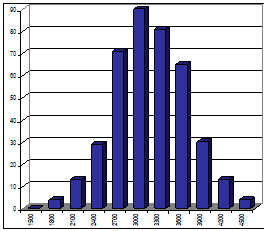
На графиках A и B даны распределения случайных величин, с одинаковым средним значением и разным стандартным отклонением.

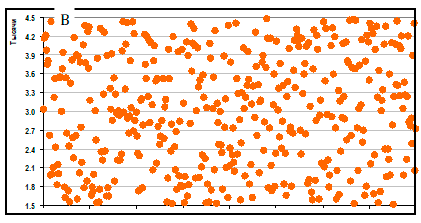
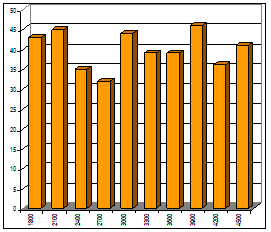
На графиках B и C даны распределения случайных величин, которые имеют одинаковые средние значения и одинаковые стандартные отклонениея, но совершенно разные функции распределения.

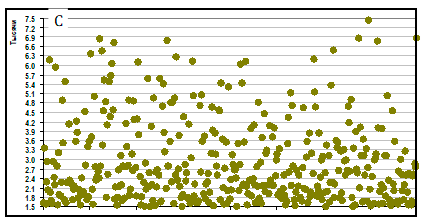
Случайные величины сильно различаются. Невозможно полно описать случайные величины даже с помощью понятий среднее значение и стандартное отклонение.

Вычисление среднедневного спроса и стандартнного отклонения

Проведем вычисления для нашей задачи.

среднедневной спрос:
d = (d₁ + d₂ + d₃ + … + d_N) / N
стандартное отклонение дневного спроса:
S_d = корень(((d₁ - d)² + (d₂ - d)² + (d₃ - d)² + ... + (d_N - d)²) / (N - 1))

среднедневной спрос:
d = СРЗНАЧ( d_i )
стандартное отклонение дневного спроса:
s_d = СТАНДОТКЛОН.В( d_i )

У нас в задаче есть данные о продажах за 100 дней. Эти данные приведены в таблице:

День	Продажи	День	Продажи	День	Продажи	День	Продажи
1	92	26	138	51	73	76	84
2	137	27	163	52	69	77	131
3	74	28	126	53	191	78	43
4	137	29	175	54	58	79	154
5	101	30	136	55	56	80	94
6	113	31	96	56	182	81	69
7	90	32	111	57	63	82	69
8	164	33	143	58	44	83	87
9	99	34	90	59	125	84	109
10	60	35	76	60	84	85	90
11	43	36	64	61	46	86	72
12	30	37	81	62	111	87	127
13	113	38	84	63	121	88	188
14	109	39	116	64	99	89	138
15	99	40	114	65	72	90	140
16	116	41	63	66	68	91	113
17	88	42	132	67	112	92	77
18	67	43	132	68	138	93	94
19	85	44	77	69	99	94	98
20	138	45	52	70	105	95	99
21	113	46	48	71	82	96	95
22	126	47	71	72	93	97	154
23	62	48	71	73	46	98	87
24	108	49	68	74	114	99	128
25	88	50	103	75	163	100	65

среднее значение спроса 100 ед. в день,
стандартное отклонение - 35.

Построим частотное распределение случайного спроса.
Для этого разобьем весь диапазон спроса на небольшое число более мелких интервалов так, чтобы в каждый из них попали какие-то точки из нашей выборки. Подсчитаем количество точек выборки, попавших в каждый такой интервал, найдем долю точек, попавших в каждый интервал и построим диаграмму частотного распределения спроса.

Площадь каждого из прямоугольников на этой диаграмме равна доли точек, попадающих в интервал, на который такой прямоугольник опирается. Очевидно, что сумма площадей всех прямоугольников на диаграмме частотного распределения равна 1.
Частотное распределение дает оценку вероятности попадания спроса в каждый из выделенных интервалов.
Попытаемся оценить риск дефицита с помощью найденного частотного распределения.
Для этого сложим площади прямоугольников, опирающихся на интервалы, находящиеся выше среднедневного спроса, т.е. выше 100 единиц:
0,18 + 0,17 + 0,5 +0,4 = 0,44
Сумма площадей этих прямоугольников, очевидно, покажет, как часто спрос превышал 100 единиц. В данном случае оказалось, что это частота равна 0,44 (44 точки из 100 вошедших в выборку лежат выше ординаты 100).
Если эту частоту, которая относится к случайной выборке из истории продаж данного товара использовать, как оценку вероятности того, что спрос превысит 100 единиц, то получается, что вопрос об оценки риска возникновения дефицита решен.
Однако, на самом деле, оценка вероятности по частоте всегда сопряжена с ошибкой, которая тем больше, чем меньше размер выборки.
Если подбрасить монету 10 раз, то вполне возможно, что орел выпадет 8 раз. Это приведет к оценке выпадения орла при подбрасывании монетки равной 0,8. Однако, если подбросить монету 100 раз, то выпадение орла 80 раз практически невозможно. И при такой статистике оценка вероятности получится гораздо ближе к 0,5.
В нашем случае, как и во многих других, для оценки распределения вероятностей различных значений НЕ НУЖНО проводить исследования частотного распределения выборочных значений. Дело в том, что если нас интересует суммарный спрос за несколько (L) дней, то его распределение заранее известно. Вспомним центральную предельную теорему теории вероятности, иллюстрацию которой мы наблюдали, когда говорили о статистическом моделировании.
Везде, где мы имеем дело с суммой случайных величин (не важно, одинаково распределенных или нет, если только одна или несколько из них не доминируют над всеми остальными), мы встречаем нормальное распределение вероятностей. Даже, если речь идет о спросе за 1 день, он весьма часто формируется благодаря множеству малых случайных факторов, и потому также распределен нормально.

вычисленного значения среднедневного спроса d = 100,
вычисленного значения стандартного отклонения s_d = 35
и знания того факта, что сумарные характеристики спроса за длинный период имеют нормальное распределения.

И это значительно упрощает нашу задачу. Вспомним, что величина безопасного резерва - это приближенная оценка, значение, которой не обязательно знать с очень большой точностью.

Рассмотрим свойства нормального распределения и используем нормальное распределение для оценки риска возникновения дефицита.

4

Оценка риска возникновения дефицита с помощью нормального распределения

Нормальное распределение для плотности вероятности случайной величины имеет вид:

где

- среднее значение случайной величины (например, ожидаемое значение случайного спроса), а s_x – ее стандартное отклонение.
Соответствующая стандартная функция Excel =НОРМ.РАСП( x,

, s_x, истина). Все нормальные кривые (с разными средними значениями и стандартными отклонениями) можно свести к одной. Если ввести величину z, равную

По смыслу z - величина отклонения спроса от его среднего значения, выраженная в единицах стандартного отклонения.
Подставив z в формулу нормального распределения мы получим стандартное нормальное распределение, не имеющее никаких параметров ( его среднее значение равно нулю, а стандартное отклонение – 1):

Это распределение приведено ниже:

Как оценить риск возникновения дефицита по нормальному распределению?

Данные нашей задачи:

Средний дневной спрос	d	100	единиц
Стандартное отклонение	s_d	35	единиц
Время ожидания поставки	L	16	дней

Среднее значение суммарного спроса за L=16 дней ожидания поставки составит

= 100 * 16 = 1600 единиц.
Cтандартное отклонение этого суммарного спроса равно

S_x = 35 * √16 = 35 * 4 = 140. При этом случайное значение суммарного спроса X_L распределено нормально.
Допустим, что менеджер на время ожидания новой партии товара оставляет на складе запас равный ROP (

= ROP).
Дефицит возникнет, если спрос превысит оставленный менеджером запас.
Вероятность этого события измеряется суммарной площадью на частотной диаграмме нормального распределения, лежащих справа от значения z=0. Очевидно, что эта площадь (площадь под правой половиной кривой нормального распределения) равна 0,5, а значит, вероятность дефицита составит 50%.

Пусть менеджер, желая снизить риск возникновения дефицита, делает перезаказ, когда запас данного товара на складе ROP >

. Пусть оставленный запас превышает величину среднего суммарного спроса за время выполнения поставки на z_α стандартных отклонений суммарного спроса за это время, т.е.

Тогда риск возникновения дефицита будет измеряться площадью под хвостом кривой нормального распределения справа от значения z_α

Таким образом, z_α показывает, какой безопасный резерв SS = z_α * s_x нужно добавить к среднему спросу за время ожидания поставки так, чтобы риск возникновения дефицита за этот период не превысил α.

Практически вычисление риска возникновения дефицита α при заданном значении точки перезаказа ROP, или, наоборот, вычисление величины безопасного резерва SS и точки перезаказа ROP при выбранном значении риска возникновения дефицита α, сводится к вычислению площадей под кривой стандартного нормального распределения.

Это вычисление легко выполнить с помощью специальных функций MS-Excel.

Функции Excel для стандартного нормального распределения
α ↔ Z_α
Z_α = Норм.Ст.Обр(1 - α )
отметим, что в качестве вероятности, запрашиваемой этой функцией, нужно подставить вероятность того, что дефицита за время ожидания поставки не будет, т.е. 1 - α.
1 - α = Норм.Ст.Расп( Z_α;1)

При этом точка перезаказа будет определяться как

_{d_L}

если задан текущий запас или уровень перезаказа ROP и надо найти вероятность дефицита α
- Z_α = (ROP - d_L) / s_{d_L} или Z_α = (ЗАПАС - d_L) / s_{d_L}
- α = 1 - НОРМ.СТ.РАСП(Z_α)
eсли задан желаемый риск дефицита α и надо найти точку перезаказа ROP
- Z = НОРМ.СТ.ОБР(1 - α)
- ROP = d_L + Z * S_{d_L}

Внесем полученные формулы в реальные модели управления запасами.

fixed order quantity system, FOQS

Заказ заранее запланированной партии товара размером

Q = d * T

делают как только на складе осталось

ROP = d * L + Z_α * s_x

единиц товара.
Re-Order Point - точка перезаказа, s_x - стандартное отклонение спроса за время поставки, а Z_α – безопасный резерв в единицах стандартных отклонений для заданного риска дефицита α.
При постоянном премени исполнения заказа L

s_x = s_d*корень(L)

fixed order interval system, FOIS

Заказ делают в заранее запланированное время, но размер заказа определяется по формуле

Q = d * T + d * L - I + Z_α * s_x

единиц товара,
т.е. расчитывается потребность в товаре на весь срок

T + L

до получения возможной коррекции запаса и из нее вычитается уже имеющийся запас I и добавляется страховой резерв .
s_x - стандартное отклонение спроса за время T + L, а Z_α – безопасный резерв в единицах стандартных отклонений для заданного риска дефицита α. При постоянном времени исполнения заказа L

s_x= s_d * корень( T + L )

Используя приведенные выше формулы, мы легко можем ответить на вопросы нашей задачи.

Риск дефицита	α	10%	5%	1%
Относительный безопасный резерв	Z_α	1,28	1,64	2,33
Абсолютный безопасный резерв, шт	SS	179	230	326
Запас на 16 дней	ROP	1779	1830	1926

На главную

Материалы лекций

Фишки MS Excel

Здесь рассматриваются следующие темы:

Кейс. Управление запасами на оптовом складе

1

Идеализированные модели управления запасами

fixed order quantity system, FOQS

fixed order interval system, FOIS

Диаграммы остатков склада в разных схемах управления запасами

2

Реальные модели управления запасами

fixed order quantity system, FOQS

fixed order interval system, FOIS

Диаграмма остатков склада при схеме управления запасами, учитывающей безопасный резерв

3

Как описать случайный спрос

Опсание случайной величины. Среднее значение и стандартное отклонение.

Сложности в описании случайных величин

Вычисление среднедневного спроса и стандартнного отклонения

4

Оценка риска возникновения дефицита с помощью нормального распределения

fixed order quantity system, FOQS

fixed order interval system, FOIS

День	Продажи	День	Продажи	День	Продажи	День	Продажи
1	92	26	138	51	73	76	84
2	137	27	163	52	69	77	131
3	74	28	126	53	191	78	43
4	137	29	175	54	58	79	154
5	101	30	136	55	56	80	94
6	113	31	96	56	182	81	69
7	90	32	111	57	63	82	69
8	164	33	143	58	44	83	87
9	99	34	90	59	125	84	109
10	60	35	76	60	84	85	90
11	43	36	64	61	46	86	72
12	30	37	81	62	111	87	127
13	113	38	84	63	121	88	188
14	109	39	116	64	99	89	138
15	99	40	114	65	72	90	140
16	116	41	63	66	68	91	113
17	88	42	132	67	112	92	77
18	67	43	132	68	138	93	94
19	85	44	77	69	99	94	98
20	138	45	52	70	105	95	99
21	113	46	48	71	82	96	95
22	126	47	71	72	93	97	154
23	62	48	71	73	46	98	87
24	108	49	68	74	114	99	128
25	88	50	103	75	163	100	65

День	Продажи	День	Продажи	День	Продажи	День	Продажи
1	92	26	138	51	73	76	84
2	137	27	163	52	69	77	131
3	74	28	126	53	191	78	43
4	137	29	175	54	58	79	154
5	101	30	136	55	56	80	94
6	113	31	96	56	182	81	69
7	90	32	111	57	63	82	69
8	164	33	143	58	44	83	87
9	99	34	90	59	125	84	109
10	60	35	76	60	84	85	90
11	43	36	64	61	46	86	72
12	30	37	81	62	111	87	127
13	113	38	84	63	121	88	188
14	109	39	116	64	99	89	138
15	99	40	114	65	72	90	140
16	116	41	63	66	68	91	113
17	88	42	132	67	112	92	77
18	67	43	132	68	138	93	94
19	85	44	77	69	99	94	98
20	138	45	52	70	105	95	99
21	113	46	48	71	82	96	95
22	126	47	71	72	93	97	154
23	62	48	71	73	46	98	87
24	108	49	68	74	114	99	128
25	88	50	103	75	163	100	65

День	Продажи	День	Продажи	День	Продажи	День	Продажи
1	92	26	138	51	73	76	84
2	137	27	163	52	69	77	131
3	74	28	126	53	191	78	43
4	137	29	175	54	58	79	154
5	101	30	136	55	56	80	94
6	113	31	96	56	182	81	69
7	90	32	111	57	63	82	69
8	164	33	143	58	44	83	87
9	99	34	90	59	125	84	109
10	60	35	76	60	84	85	90
11	43	36	64	61	46	86	72
12	30	37	81	62	111	87	127
13	113	38	84	63	121	88	188
14	109	39	116	64	99	89	138
15	99	40	114	65	72	90	140
16	116	41	63	66	68	91	113
17	88	42	132	67	112	92	77
18	67	43	132	68	138	93	94
19	85	44	77	69	99	94	98
20	138	45	52	70	105	95	99
21	113	46	48	71	82	96	95
22	126	47	71	72	93	97	154
23	62	48	71	73	46	98	87
24	108	49	68	74	114	99	128
25	88	50	103	75	163	100	65